栈

栈

栈的介绍

栈（Stack）：也叫做堆栈，一种遵循后进先出LIFO(Last In First Out)策略的线性数据结构。只允许在一端进行插入与删除操作，这一端称为栈顶（top）。常用于函数调用管理、表达式求值、括号匹配、回溯等场景。

  • 优势

    • 操作语义简单，接口小巧
    • 入栈/出栈时间复杂度理想（O(1) 摊还/均摊）
    • 适合实现回溯、撤销等场景

  • 劣势

    • 访问受限，仅能访问栈顶

    • 顺序栈可能需要扩容策略；链栈每次操作都有分配/释放开销

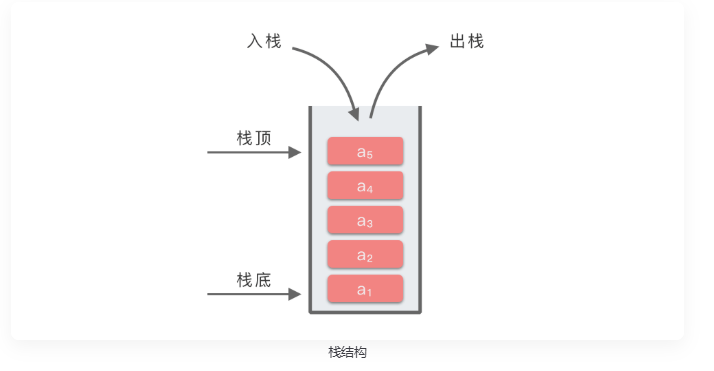
我们可以把栈想象成一摞叠放的盘子：

  • 栈顶（top）：可以插入和删除元素的一端，就像盘子堆的最上面。
  • 栈底（bottom）：固定不动的一端，不能进行操作，就像盘子堆的最下面。
  • 空栈：栈中没有任何元素时，称为空栈。

基本操作

栈的常见操作有：

  • 入栈（Push）：在栈顶加入一个新元素。

  • 出栈（Pop）：移除并返回栈顶的元素。

  • 查看栈顶（Peek）：只查看栈顶元素，但不移除。

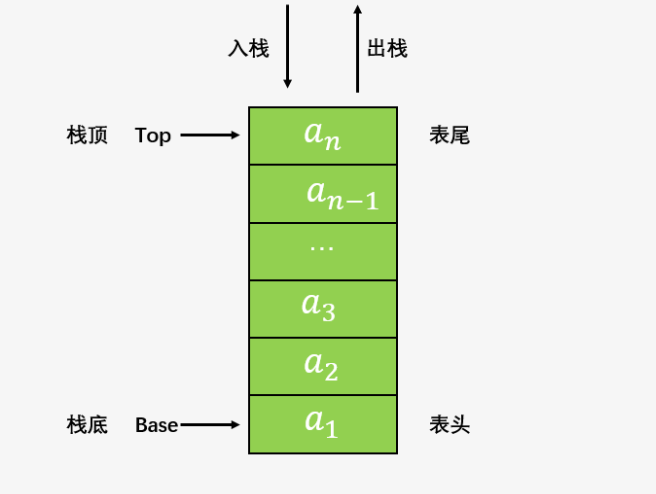
下图展示了栈的结构和操作方式：

image-20251023144742151

栈的实现方式

与线性表类似，栈常见的存储方式有两种：顺序栈 和 链式栈。

  • 顺序栈：采用一段连续的存储空间（==数组==）依次存放从栈底到栈顶的元素，并通过指针top标记当前栈顶元素在数组中的位置。
  • 链式栈：采用==单链表==实现，每次新元素都插入到链表头部，top始终指向链表的头节点，即栈顶元素的位置。

顺序栈(数组实现)

栈的最常见实现方式是利用数组来构建顺序存储结构。这种基于顺序存储的栈结构，通常被称为顺序栈。

image-20251030140220439

静态顺序栈

栈结构体定义

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
/**
 * @brief 元素类型定义
 */
typedef int ElemType;

/**
 * @brief 栈的最大容量（固定）
 */
#define MAX_SIZE 100

/**
 * @brief 栈容器（静态顺序表结构体）
 */
typedef struct Stack {
    ElemType data[MAX_SIZE]; /**< 固定容量缓冲区，索引范围 [0, MAX_SIZE-1] */
    int      top;            /**< 下一个可写位置（亦为当前元素个数）；空栈为 0，栈顶元素在 data[top-1] */
} Stack;

静态栈的实现不涉及动态扩容，只需要我们一个固定大小的数组和一个栈顶指针即可构成Stack的结构体

API设计

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
/*  基础管理 */
void stack_init(Stack* s);
void stack_destroy(Stack* s);
/*  状态查询  */
size_t stack_size(const Stack* s);
bool stack_empty(const Stack* s);
bool stack_full(const Stack* s);

/* 栈操作  */
bool stack_push(Stack* s, ElemType value);
bool stack_pop(Stack* s, ElemType* out_value);
bool stack_top(const Stack* s, ElemType* out_value);

/*  调试/遍历 */
void stack_print(const Stack* s);
void stack_foreach(const Stack* s, void (*fn)(ElemType value, void* user), void* user);

/* ========================= 兼容接口（静态容量） ========================= */
bool stack_reserve(Stack* s, size_t new_cap);
void stack_shrink_to_fit(Stack* s);

静态顺序栈源码实现

github源码：https://github.com/keqiudi/Stack/tree/master/Sequential_Stack/static_stack

static_stack.h
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
/**
 * @file    stack.h
 * @brief   基于静态顺序表（定长数组，ElemType 元素）的栈接口声明
 * @details 提供栈的初始化、销毁、入栈/出栈/取顶、判空/判满/取大小、遍历与打印等操作；默认线程不安全。
 *          本实现采用固定容量 MAX_SIZE 的顺序栈，不进行动态分配与扩容。
 *          栈顶索引采用“下一个可写位置”约定：空栈 top==0，非空时栈顶元素位于 data[top-1]。
 *
 * @note    复杂度（静态顺序栈）：
 *          - 入栈 push、出栈 pop、取顶 top、判空/判满/取大小：O(1)
 *          - 遍历 foreach、打印 print：O(n)
 *          - 预留容量/收缩容量：不适用（静态容量）；提供占位接口，时间 O(1)
 */

#ifndef STACK_H
#define STACK_H

#include <stdbool.h>  /* bool   */
#include <stddef.h>   /* size_t */

#ifdef __cplusplus
extern "C" {
#endif

typedef int ElemType;

/**
 * @brief 栈的最大容量（固定）
 */
#define MAX_SIZE 100

/**
 * @brief 栈容器（静态顺序表实现）
 */
typedef struct Stack {
    ElemType data[MAX_SIZE]; /**< 固定容量缓冲区，索引范围 [0, MAX_SIZE-1] */
    int      top;            /**< 下一个可写位置（亦为当前元素个数）；空栈为 0，栈顶元素在 data[top-1] */
} Stack;

/* ======================= 基础管理 ======================= */

/**
 * @brief  初始化栈（置空）
 * @param  s 指向栈对象
 * @note   空栈时 top=0
 */
void stack_init(Stack* s);

/**
 * @brief  销毁栈（静态实现，无需释放内存）
 * @param  s 指向栈对象
 * @note   等价于重置为空：top=0
 */
void stack_destroy(Stack* s);

/* ======================= 状态查询 ======================= */

/**
 * @brief  获取当前元素个数
 * @param  s 指向栈对象（可为 NULL）
 * @return 元素个数；若 s 为 NULL 返回 0
 */
size_t stack_size(const Stack* s);

/**
 * @brief  判断栈是否为空
 * @param  s 指向栈对象
 * @return 为空返回 true，否则返回 false
 * @note   判空等价于 (top == 0)
 */
bool stack_empty(const Stack* s);

/**
 * @brief  判断栈是否已满
 * @param  s 指向栈对象
 * @return 已满返回 true，否则返回 false
 * @note   判满等价于 (top == MAX_SIZE)
 */
bool stack_full(const Stack* s);

/* ========================= 栈操作 ========================= */

/**
 * @brief  入栈：将元素压入栈顶
 * @param  s     栈指针
 * @param  value 待入栈的值
 * @return 成功返回 true；满栈或参数无效返回 false
 * @complexity O(1)
 * @note   写入 data[top] 后 top++；满栈（top==MAX_SIZE）时操作失败
 */
bool stack_push(Stack* s, ElemType value);

/**
 * @brief  出栈：弹出栈顶元素
 * @param  s         栈指针
 * @param  out_value 若非 NULL，则返回被弹出的值
 * @return 成功返回 true；空栈或参数无效返回 false
 * @complexity O(1)
 * @note   先 --top，再读取 data[top]
 */
bool stack_pop(Stack* s, ElemType* out_value);

/**
 * @brief  取栈顶元素（不弹出）
 * @param  s         栈指针（只读）
 * @param  out_value 若非 NULL，则返回栈顶值
 * @return 成功返回 true；空栈或参数无效返回 false
 * @complexity O(1)
 * @note   读取 data[top-1]；调用前需确保非空
 */
bool stack_top(const Stack* s, ElemType* out_value);

/* ========================= 调试/遍历 ========================= */

/**
 * @brief  打印栈内容（调试用途）
 * @param  s 栈指针
 * @note   建议输出格式：[a, b, c] top=c (size=n, cap=MAX_SIZE)
 */
void stack_print(const Stack* s);

/**
 * @brief  遍历栈（自底向上），对每个元素调用回调
 * @param  s    栈指针
 * @param  fn   回调函数：void (*)(ElemType value, void* user)
 * @param  user 透传给回调的用户参数
 * @note   回调内若修改栈需谨慎，避免破坏遍历过程
 */
void stack_foreach(const Stack* s, void (*fn)(ElemType value, void* user), void* user);

/* ========================= 兼容接口（静态容量） ========================= */

/**
 * @brief  预留容量（静态顺序栈不可扩容）
 * @param  s       栈指针（忽略）
 * @param  new_cap 期望容量
 * @return 当 new_cap <= MAX_SIZE 返回 true；否则返回 false
 * @complexity O(1)
 * @note   兼容动态栈接口，静态实现仅用于能力探测
 */
bool stack_reserve(Stack* s, size_t new_cap);

/**
 * @brief  收缩容量（静态顺序栈无效操作）
 * @param  s 栈指针（忽略）
 * @complexity O(1)
 * @note   兼容动态栈接口，静态实现不进行任何操作
 */
void stack_shrink_to_fit(Stack* s);

#ifdef __cplusplus
}
#endif

#endif /* STACK_H */
static_stack.c
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
//
// Created by keqiu on 25-10-23.
//

#include "stack.h"
#include "stdio.h"


/* 初始化 */
void stack_init(Stack* s)
{
    if (s == NULL)
    {
        return;
    }

    s->top = 0;
}

/* 静态顺序栈无需释放堆内存，这里等价清空 */
void stack_destroy(Stack* s)
{
    if (s == NULL)
    {
        return;
    }

    s->top = 0;

}

size_t stack_size(const Stack* s)
{
    if (s == NULL)
    {
        return 0;
    }

    return (size_t)s->top;
}

bool stack_empty(const Stack* s)
{
    if (s == NULL)
    {
        return true;
    }

    return s->top == 0;
}

bool stack_full(const Stack* s)
{
    if (s == NULL)
    {
        return false;
    }

    return s->top == MAX_SIZE;
}

bool stack_push(Stack* s, ElemType value)
{
    if (s == NULL)
    {
        return false;
    }

    if (stack_full(s))
    {
        return false;
    }

    s->data[s->top] = value;
    s->top++;

    return true;
}

bool stack_pop(Stack* s, ElemType* out_value)
{
    if (s == NULL)
    {
        return false;
    }

    if (stack_empty(s))
    {
        return false;
    }

    s->top--;
    *out_value = s->data[s->top];

    return true;
}

bool stack_top(const Stack* s, ElemType* out_value)
{
    if (s == NULL)
    {
        return false;
    }

    if (stack_empty(s))
    {
        return false;
    }

    *out_value = s->data[s->top-1];

    return true;
}

/* 调试输出：自底向上显示，标注 size/cap 与 top 值 */
void stack_print(const Stack* s) {
    if (s == NULL || stack_empty(s)) {
        printf("[] top=? (size=0, cap=%d)\n", (int)MAX_SIZE);
        return;
    }
    printf("[");
    for (int i = 0; i < s->top; ++i) {
        printf("%d", s->data[i]);
        if (i + 1 < s->top) printf(", ");
    }
    printf("] top=%d (size=%zu, cap=%d)\n",
           s->data[s->top - 1], stack_size(s), (int)MAX_SIZE);
}

void stack_foreach(const Stack* s, void (*fn)(ElemType value, void* user), void* user)
{
    if (!s || !fn) return;

    for (int i = 0; i < s->top; ++i) {
        fn(s->data[i], user);
    }
}

bool stack_reserve(Stack* s, size_t new_cap)
{
    (void)s;
    return new_cap <= MAX_SIZE;
}

void stack_shrink_to_fit(Stack* s)
{
    (void)s;
}

测试代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
#include "stack.h"
#include <stdio.h>
#include <assert.h>

/* foreach 求和回调 */
static void sum_cb(int v, void* user) {
    int* acc = (int*)user;
    *acc += v;
}

int main(void) {
    Stack s;
    stack_init(&s);

    /* 空栈状态 */
    assert(stack_empty(&s) == true);
    assert(stack_size(&s) == 0);
    assert(stack_full(&s) == false);

    int tmp;
    assert(stack_pop(&s, &tmp) == false);
    assert(stack_top(&s, &tmp) == false);

    /* 基本入栈 */
    assert(stack_push(&s, 1) == true);
    assert(stack_push(&s, 2) == true);
    assert(stack_push(&s, 3) == true);
    stack_print(&s);                        /* [1,2,3] top=3 */
    assert(stack_size(&s) == 3);
    assert(stack_empty(&s) == false);

    /* 取顶不弹出 */
    int topv = 0;
    assert(stack_top(&s, &topv) == true);
    printf("top=%d\n", topv);
    assert(topv == 3);

    /* 出栈与顺序校验（LIFO） */
    int v = 0;
    assert(stack_pop(&s, &v) == true);      /* 弹 3 */
    assert(v == 3);
    stack_print(&s);

    assert(stack_pop(&s, &v) == true);      /* 弹 2 */
    assert(v == 2);
    stack_print(&s);

    assert(stack_push(&s, 99) == true);     /* 入 99 => [1,99] */
    stack_print(&s);

    /* 预留/收缩（静态容量语义） */
    assert(stack_reserve(&s, 10) == true);
    assert(stack_reserve(&s, MAX_SIZE) == true);
    assert(stack_reserve(&s, MAX_SIZE + 1) == false);
    stack_shrink_to_fit(&s); /* 无操作 */

    /* 填满到容量上限 */
    while (!stack_full(&s)) {
        int next = (int)stack_size(&s);
        assert(stack_push(&s, next) == true);
    }
    stack_print(&s);
    assert(stack_full(&s) == true);
    assert(stack_size(&s) == MAX_SIZE);

    /* 满栈再 push 失败 */
    assert(stack_push(&s, 12345) == false);

    /* 出栈几个，校验 LIFO */
    assert(stack_pop(&s, &v) == true);
    assert(stack_pop(&s, &v) == true);
    assert(stack_pop(&s, &v) == true);
    stack_print(&s);

    /* foreach 求和（自底向上） */
    int sum = 0;
    stack_foreach(&s, sum_cb, &sum);
    printf("sum=%d\n", sum);

    /* 销毁（等价清空） */
    stack_destroy(&s);
    assert(stack_empty(&s) == true);
    assert(stack_size(&s) == 0);
    stack_print(&s);

    printf("All tests passed!\n");
    return 0;
}

输出结果如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
C:\Users\keqiu\myProjects\CLionProjects\C\Stack\Sequential_Stack\static_stack\build\Stack.exe
    
[1, 2, 3] top=3 (size=3, cap=100)
top=3
[1, 2] top=2 (size=2, cap=100)
[1] top=1 (size=1, cap=100)
[1, 99] top=99 (size=2, cap=100)
[1, 99, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31,
32, 33, 34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 49, 50, 51, 52, 53, 54, 55, 56, 57, 58, 59, 60, 61,
62, 63, 64, 65, 66, 67, 68, 69, 70, 71, 72, 73, 74, 75, 76, 77, 78, 79, 80, 81, 82, 83, 84, 85, 86, 87, 88, 89, 90, 91,
92, 93, 94, 95, 96, 97, 98, 99] top=99 (size=100, cap=100)
[1, 99, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31,
32, 33, 34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 49, 50, 51, 52, 53, 54, 55, 56, 57, 58, 59, 60, 61,
62, 63, 64, 65, 66, 67, 68, 69, 70, 71, 72, 73, 74, 75, 76, 77, 78, 79, 80, 81, 82, 83, 84, 85, 86, 87, 88, 89, 90, 91,
92, 93, 94, 95, 96] top=96 (size=97, cap=100)
sum=4755
[] top=? (size=0, cap=100)
All tests passed!

动态顺序栈

栈结构体定义

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
/**
 * @typedef ElemType
 * @brief   栈中元素类型。
 */
typedef int ElemType;

/**
 * @def DEFAULT_CAPACITY
 * @brief 初始容量下限。
 * @note  初始化时若默认分配失败，`capacity==0`，后续在 `push/reserve` 时再尝试分配。
 */
#define DEFAULT_CAPACITY 16

/**
 * @struct Stack
 * @brief  动态顺序栈。
 *
 * - `data` 指向连续存储区，长度为 `capacity`；
 * - `top` 为当前元素个数，范围 \[0, capacity\]；
 * - `capacity` 为当前可容纳的元素数。
 */
typedef struct Stack
{
    ElemType* data;     /**< 动态缓冲区首址；可能为 NULL（尚未或已释放） */
    size_t    top;      /**< 栈顶指针(当前元素个数)；空栈为 0，栈顶元素在 data[top-1] */
    size_t    capacity; /**< 当前容量（`data` 可容纳的元素数） */
} Stack;

由于动态栈的实现种涉及到动态扩容，所以我们将固定大小的数组换成了一个指向这块数据内存的首地址的指针和一个可以记录容量的变量

我们仍然可以通过访问数组的方式访问这个指针，如：stack->data[stack->top-1]就是访问栈顶元素的数据

API设计

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
/*  基础管理 */
void stack_init(Stack* s);
void stack_destroy(Stack* s);
/*  状态查询  */
size_t stack_size(const Stack* s);
bool stack_empty(const Stack* s);
bool stack_full(const Stack* s);

/* 栈操作  */
bool stack_push(Stack* s, ElemType value);
bool stack_pop(Stack* s, ElemType* out_value);
bool stack_top(const Stack* s, ElemType* out_value);

/*  调试/遍历 */
void stack_print(const Stack* s);
void stack_foreach(const Stack* s, void (*fn)(ElemType value, void* user), void* user);

/* ========================= 兼容接口（静态容量） ========================= */
bool stack_reserve(Stack* s, size_t new_cap);

void stack_shrink_to_fit(Stack* s);

动态顺序栈源码实现

github源码：https://github.com/keqiudi/Stack/tree/master/Sequential_Stack/dynamic_stack

dynamic_stack.h
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
// stack.h
#pragma once

/**
 * @file    stack.h
 * @brief   动态顺序栈（可自动扩容，倍增策略）
 *
 * 提供对整型元素的入栈、出栈、取顶、遍历与容量管理接口。
 * 采用连续内存（顺序表）存储，扩容使用 2x 倍增以获得摊还 O(1) 的入栈性能。
 */

#ifndef STACK_H
#define STACK_H

#include <stdbool.h>
#include <stddef.h>

#ifdef __cplusplus
extern "C" {
#endif

/**
 * @typedef ElemType
 * @brief   栈中元素类型。
 */
typedef int ElemType;

/**
 * @def DEFAULT_CAPACITY
 * @brief 初始容量下限。
 * @note  初始化时若默认分配失败，`capacity==0`，后续在 `push/reserve` 时再尝试分配。
 */
#define DEFAULT_CAPACITY 16

/**
 * @struct Stack
 * @brief  动态顺序栈。
 *
 * - `data` 指向连续存储区，长度为 `capacity`；
 * - `top` 为当前元素个数，范围 \[0, capacity\]；
 * - `capacity` 为当前可容纳的元素数。
 */
typedef struct Stack
{
    ElemType* data;     /**< 动态缓冲区首址；可能为 NULL（尚未或已释放） */
    size_t    top;      /**< 栈顶指针(当前元素个数)；空栈为 0，栈顶元素在 data[top-1] */
    size_t    capacity; /**< 当前容量（`data` 可容纳的元素数） */
} Stack;

/* ======================= 基础管理 ======================= */

/**
 * @brief  初始化栈，并尽力分配默认容量。
 * @param  s 栈指针，不能为空。
 * @note   分配失败时保持可用的“空栈”语义：`data==NULL`、`top==0`、`capacity==0`。
 * @complexity O(1)
 */
void stack_init(Stack* s);

/**
 * @brief  销毁栈，释放堆内存并复位为“空栈”。
 * @param  s 栈指针，可为 NULL（安全无操作）。
 * @complexity O(1)
 */
void stack_destroy(Stack* s);

/* ======================= 状态查询 ======================= */

/**
 * @brief  获取当前元素个数。
 * @param  s 栈指针，可为 NULL。
 * @return 若 `s==NULL` 返回 0，否则返回 `s->top`。
 * @complexity O(1)
 */
size_t stack_size(const Stack* s);

/**
 * @brief  判断是否为空栈（`top==0`）。
 * @param  s 栈指针；若为 NULL，返回 false。
 * @return 空返回 true；`s==NULL` 或非空返回 false。
 * @complexity O(1)
 */
bool stack_empty(const Stack* s);

/**
 * @brief  判断是否已到当前容量上限（`top==capacity`）。
 * @param  s 栈指针；若为 NULL，返回 false。
 * @return 满返回 true；否则返回 false。
 * @note   动态模式下“满”仅表示到达当前容量，可扩容后继续使用。
 * @complexity O(1)
 */
bool stack_full(const Stack* s);

/* ========================= 栈操作 ========================= */

/**
 * @brief  入栈；容量不足时自动扩容（倍增）。
 * @param  s     栈指针，不能为空。
 * @param  value 待入栈的元素值。
 * @return 成功返回 true；若分配失败或 `s==NULL` 返回 false（不改变原状态）。
 * @complexity 摊还 O(1)；扩容发生时为 O(n) 拷贝。
 */
bool stack_push(Stack* s, ElemType value);

/**
 * @brief  出栈；可选返回被弹出的元素。
 * @param  s         栈指针。
 * @param  out_value 若非 NULL，写回弹出的元素值。
 * @return 成功返回 true；若 `s==NULL` 或空栈返回 false。
 * @complexity O(1)
 */
bool stack_pop(Stack* s, ElemType* out_value);

/**
 * @brief  读取栈顶元素但不弹出。
 * @param  s         栈指针。
 * @param  out_value 若非 NULL，写回栈顶元素值。
 * @return 成功返回 true；若 `s==NULL` 或空栈返回 false。
 * @complexity O(1)
 */
bool stack_top(const Stack* s, ElemType* out_value);

/* ========================= 调试/遍历 ========================= */

/**
 * @brief  打印栈内容（自底向上），用于调试。
 * @param  s 栈指针；若为 NULL 或空栈，打印空表示。
 * @note   输出包含元素序列、栈顶元素、`top`、`capacity`。
 */
void stack_print(const Stack* s);

/**
 * @brief  自底向上遍历所有元素，并调用回调。
 * @param  s   栈指针；若为 NULL 则无操作。
 * @param  fn  回调函数指针，不能为空；形如 `void (*fn)(ElemType value, void* user)`。
 * @param  user 透传的用户上下文指针，可为 NULL。
 * @note   回调按索引递增顺序调用。
 * @complexity O(n)
 */
void stack_foreach(const Stack* s, void (*fn)(ElemType value, void* user), void* user);

/* ========================= 容量管理 ========================= */

/**
 * @brief  预留容量到不小于 `new_cap`。
 * @param  s       栈指针，不能为空。
 * @param  new_cap 期望容量（元素个数）。
 * @return 若当前容量已满足或扩容成功返回 true；内存分配失败返回 false。
 * @note   不改变 `top`；若 `new_cap <= capacity` 直接返回 true。
 * @complexity 可能触发一次 O(n) 重新分配与拷贝。
 */
bool stack_reserve(Stack* s, size_t new_cap);

/**
 * @brief  收缩容量到恰好 `top`。
 * @param  s 栈指针；若为 NULL 无操作。
 * @note   当 `top==0` 时释放缓冲区（变为“空栈”）。若收缩失败则保持原状。
 * @complexity 可能触发一次 O(n) 重新分配与拷贝。
 */
void stack_shrink_to_fit(Stack* s);

#ifdef __cplusplus
}
#endif

#endif /* STACK_H */
dynamic_stack.c
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
//
// Created by keqiu on 25-10-27.
//
// stack.c
#include "stack.h"
#include <stdlib.h>
#include <stdio.h>

/* 计算新的容量：至少满足 need，倾向于倍增 */
static size_t calc_grow_capacity(size_t old_cap, size_t need)
{
    /* 如果没有容量，先使用默认容量*/
    if (old_cap == 0)
    {
        size_t cap = DEFAULT_CAPACITY;
        return (cap >= need) ? cap : need;
    }

    size_t new_cap = old_cap;
    while (new_cap < need)
    {
        size_t expanded_cap = new_cap << 1; // 扩充为原来容量的2倍
        if (expanded_cap <= new_cap) /* 溢出保护，移除后为负数，直接扩充为需要的容量即可 */
        {
            new_cap = need;
            break;
        }
        new_cap = expanded_cap;
    }
    return new_cap;
}

void stack_init(Stack* s)
{
    if (s == NULL)
    {
        return;
    }
    s->data = NULL;
    s->top = 0;
    s->capacity = 0;

    /* 尝试分配默认容量（失败也可延迟到 push/reserve 再尝试） */
    ElemType* default_mem = (ElemType*)malloc(sizeof(ElemType) * DEFAULT_CAPACITY);
    if (default_mem)
    {
        s->data = default_mem ;
        s->capacity = DEFAULT_CAPACITY; // 分配成功，保存内存指针和更新容量
    }
}

void stack_destroy(Stack* s) {

    if (s == NULL)
    {
        return;
    }

    free(s->data);
    s->data = NULL;
    s->top = 0;
    s->capacity = 0;
}

size_t stack_size(const Stack* s)
{
    return s ? s->top : 0;
}

bool stack_empty(const Stack* s)
{
    if (s == NULL)
    {
        return false;
    }
    return s->top == 0;
}

bool stack_full(const Stack* s)
{
    if (s == NULL)
    {
        return false;
    }

    return s->top == s->capacity;
}

static bool ensure_capacity(Stack* s, size_t need)
{
    /* 1.容量够的话直接返回 */
    if (s->capacity >= need)
    {
        return true;
    }

    /* 2.获取新容量的大小，调用realloc重新分配内存 */
    size_t new_cap = calc_grow_capacity(s->capacity, need);
    ElemType* new_mem = (ElemType*)realloc(s->data, sizeof(ElemType) * new_cap); /* 扩充内存或者重新分配*/
    if (new_mem == NULL)
    {
        return false;
    }

    s->data = new_mem;
    s->capacity = new_cap;
    return true;
}

bool stack_push(Stack* s, ElemType value)
{
    if (s == NULL)
    {
        return false;
    }

    if (ensure_capacity(s, s->top + 1) == false)
    {
        return false;
    }

    s->data[s->top] = value;
    s->top++;

    return true;
}

bool stack_pop(Stack* s, ElemType* out_value)
{
    if (s == NULL || stack_empty(s))
    {
        return false;
    }

    --s->top;
    ElemType elem_value = s->data[s->top];
    if (out_value)
    {
        *out_value = elem_value;
    }
    return true;
}

bool stack_top(const Stack* s, ElemType* out_value)
{
    if (s == NULL || stack_empty(s))
    {
        return false;
    }
    if (out_value)
    {
        *out_value = s->data[s->top - 1];
    }
    return true;
}

void stack_print(const Stack* s)
{
    if (s == NULL || s->top == 0) {
        printf("[] top=? (size=0, cap=%zu)\n", s ? s->capacity : (size_t)0);
        return;
    }
    printf("[");
    for (size_t i = 0; i < s->top; ++i) {
        printf("%d", s->data[i]);
        if (i + 1 < s->top) printf(", ");
    }
    printf("] top=%d (size=%zu, cap=%zu)\n",
           s->data[s->top - 1], s->top, s->capacity);
}

void stack_foreach(const Stack* s, void (*fn)(ElemType value, void* user), void* user)
{
    if (s == NULL || !fn) return;
    for (size_t i = 0; i < s->top; ++i)
    {
        fn(s->data[i], user);
    }
}

bool stack_reserve(Stack* s, size_t new_cap)
{
    if (s == NULL )
    {
        return false;
    }

    if (new_cap <= s->capacity)
    {
        return true;
    }
    ElemType* new_mem = (ElemType*)realloc(s->data, sizeof(ElemType) * new_cap);
    if (new_mem == NULL)
    {
        return false;
    }
    s->data = new_mem;
    s->capacity = new_cap;
    return true;
}

void stack_shrink_to_fit(Stack* s)
{
    if (s == NULL)
    {
        return;
    }

    if (s->top == s->capacity) // 栈顶刚好到容量
    {
        return;
    }

    if (s->top == 0) // 栈中没有元素
    {
        free(s->data);
        s->data = NULL;
        s->capacity = 0;
        return;
    }

    ElemType* p = (ElemType*)realloc(s->data, sizeof(ElemType) * s->top); // 收缩到刚好填满所有栈的容量
    if (p == NULL)
    {
        return; /* 收缩失败则保持原状 */
    }
    s->data = p;
    s->capacity = s->top;
}

测试代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
// main.c
#include "stack.h"
#include <stdio.h>
#include <assert.h>

/* foreach 求和回调 */
static void sum_cb(int v, void* user) {
    int* acc = (int*)user;
    *acc += v;
}

int main(void) {
    Stack s;
    stack_init(&s);

    /* 空栈状态 */
    assert(stack_empty(&s) == true);
    assert(stack_size(&s) == 0);
    assert(stack_full(&s) == false); /* 初始容量可能为 DEFAULT_CAPACITY */

    int tmp;
    assert(stack_pop(&s, &tmp) == false);
    assert(stack_top(&s, &tmp) == false);

    /* 基本入栈 */
    assert(stack_push(&s, 1) == true);
    assert(stack_push(&s, 2) == true);
    assert(stack_push(&s, 3) == true);
    stack_print(&s);                        /* [1, 2, 3] */
    assert(stack_size(&s) == 3);
    assert(stack_empty(&s) == false);

    /* 取顶不弹出 */
    int topv = 0;
    assert(stack_top(&s, &topv) == true);
    printf("top=%d\n", topv);
    assert(topv == 3);

    /* 出栈与顺序校验（LIFO） */
    int v = 0;
    assert(stack_pop(&s, &v) == true);      /* 弹 3 */
    assert(v == 3);
    stack_print(&s);

    assert(stack_pop(&s, &v) == true);      /* 弹 2 */
    assert(v == 2);
    stack_print(&s);

    assert(stack_push(&s, 99) == true);     /* 入 99 => [1,99] */
    stack_print(&s);

    /* 预留与收缩（动态容量语义） */
    assert(stack_reserve(&s, 10) == true);
    size_t cap_before = s.capacity;
    assert(cap_before >= 10);

    assert(stack_reserve(&s, 100) == true);
    assert(s.capacity >= 100);

    stack_shrink_to_fit(&s);
    assert(s.capacity == s.top);            /* 收缩到刚好 top */

    /* 自动扩容：填充到 200 个元素 */
    while (stack_size(&s) < 200)
    {
        int next = (int)stack_size(&s);
        assert(stack_push(&s, next) == true);
    }
    stack_print(&s);
    assert(stack_size(&s) == 200);
    assert(s.capacity >= 200);

    /* 出栈几个，校验 LIFO */
    assert(stack_pop(&s, &v) == true);
    assert(stack_pop(&s, &v) == true);
    assert(stack_pop(&s, &v) == true);
    stack_print(&s);

    /* foreach 求和（自底向上） */
    int sum = 0;
    stack_foreach(&s, sum_cb, &sum);
    printf("sum=%d\n", sum);

    /* 销毁（等价清空并释放内存） */
    stack_destroy(&s);
    assert(stack_empty(&s) == true);
    assert(stack_size(&s) == 0);
    stack_print(&s);

    printf("All tests passed!\n");
    return 0;
}

输出结果如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
C:\Users\keqiu\myProjects\CLionProjects\C\Stack\Sequential_Stack\dynamic_stack\build\dynamic_stack.exe
    
[1, 2, 3] top=3 (size=3, cap=16)
top=3
[1, 2] top=2 (size=2, cap=16)
[1] top=1 (size=1, cap=16)
[1, 99] top=99 (size=2, cap=16)
[1, 99, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31,
32, 33, 34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 49, 50, 51, 52, 53, 54, 55, 56, 57, 58, 59, 60, 61,
62, 63, 64, 65, 66, 67, 68, 69, 70, 71, 72, 73, 74, 75, 76, 77, 78, 79, 80, 81, 82, 83, 84, 85, 86, 87, 88, 89, 90, 91,
92, 93, 94, 95, 96, 97, 98, 99, 100, 101, 102, 103, 104, 105, 106, 107, 108, 109, 110, 111, 112, 113, 114, 115, 116, 117
, 118, 119, 120, 121, 122, 123, 124, 125, 126, 127, 128, 129, 130, 131, 132, 133, 134, 135, 136, 137, 138, 139, 140, 141
, 142, 143, 144, 145, 146, 147, 148, 149, 150, 151, 152, 153, 154, 155, 156, 157, 158, 159, 160, 161, 162, 163, 164, 165
, 166, 167, 168, 169, 170, 171, 172, 173, 174, 175, 176, 177, 178, 179, 180, 181, 182, 183, 184, 185, 186, 187, 188, 189
, 190, 191, 192, 193, 194, 195, 196, 197, 198, 199] top=199 (size=200, cap=256)
[1, 99, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31,
32, 33, 34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 49, 50, 51, 52, 53, 54, 55, 56, 57, 58, 59, 60, 61,
62, 63, 64, 65, 66, 67, 68, 69, 70, 71, 72, 73, 74, 75, 76, 77, 78, 79, 80, 81, 82, 83, 84, 85, 86, 87, 88, 89, 90, 91,
92, 93, 94, 95, 96, 97, 98, 99, 100, 101, 102, 103, 104, 105, 106, 107, 108, 109, 110, 111, 112, 113, 114, 115, 116, 117
, 118, 119, 120, 121, 122, 123, 124, 125, 126, 127, 128, 129, 130, 131, 132, 133, 134, 135, 136, 137, 138, 139, 140, 141
, 142, 143, 144, 145, 146, 147, 148, 149, 150, 151, 152, 153, 154, 155, 156, 157, 158, 159, 160, 161, 162, 163, 164, 165
, 166, 167, 168, 169, 170, 171, 172, 173, 174, 175, 176, 177, 178, 179, 180, 181, 182, 183, 184, 185, 186, 187, 188, 189
, 190, 191, 192, 193, 194, 195, 196] top=196 (size=197, cap=256)
sum=19405
[] top=? (size=0, cap=0)
All tests passed!

链式栈

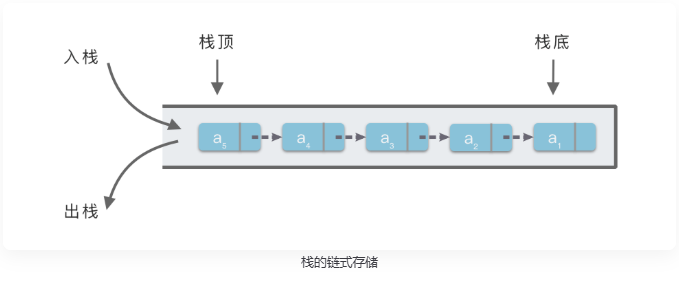
静态顺序栈在存储空间上存在一定局限性：当栈满或需要扩容时，往往需要移动大量元素，效率较低。为了解决这一问题，可以采用链式存储结构实现栈

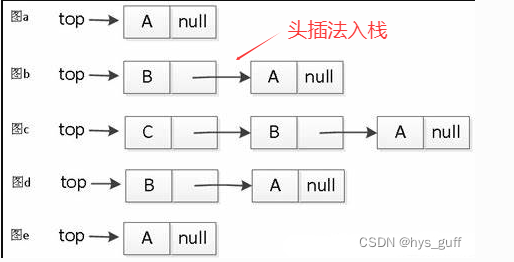
链式栈本质上就是一个链表，保存着栈顶指针top(链表头结点)，每次入栈就是执行一次头插法插入元素

image-20251030152321532

image-20251030142741515

链式栈结构体定义

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
/** 栈元素类型（可按需修改为自定义结构体/其他标量类型） */
typedef int ElemType;

/**
 * @brief 链式栈节点
 */
typedef struct LStackNode
{
    ElemType data;             /**< 节点数据域 */
    struct LStackNode* next;   /**< 指向下一个节点（更“低”的栈元素）；栈顶节点的 next 指向次顶节点 */
} LStackNode;

/**
 * @brief 链式栈容器
 */
typedef struct LStack
{
    LStackNode* top;  /**< 栈顶指针：指向当前“最上方”的节点；空栈为 NULL */
    size_t      size; /**< 当前元素个数 */
} LStack;

链式栈的每个结点LStackNode由 结点数据域(data)和 指向下一个结点的指针(struct LStackNode* next)构成

链式栈LStack保存着栈顶指针 top(链表头结点) 和 元素个数(size)

API设计

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
/*  基础管理与状态  */
void lstack_init(LStack* s);
void lstack_destroy(LStack* s);

/*  状态查询  */
size_t lstack_size(const LStack* s);
bool lstack_empty(const LStack* s);

/*  栈操作  */
bool lstack_push(LStack* s, ElemType value);
bool lstack_pop(LStack* s, ElemType* out_value);
bool lstack_top(const LStack* s, ElemType* out_value);

/*  调试/遍历  */
void lstack_print(const LStack* s);
void lstack_foreach(const LStack* s, void (*fn)(ElemType value, void* user), void* user);

api设计与链表和顺序栈类似，只不过链式栈没有判断栈满的api

链式栈源码实现

github源码：Stack/Linked_Stack at master · keqiudi/Stack

linked_stack.h

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
/**
 * @file    stack.h
 * @brief   链式栈（单链表实现）接口声明
 * @details 提供链式栈的初始化、销毁、入栈/出栈/取顶、判空/取大小、遍历与打印等操作。
 *          - 栈顶 top 指向单链表的第一个节点；空栈时 top==NULL，size==0。
 *          - 链式栈容量仅受内存限制，入栈会动态分配节点内存，出栈会释放节点内存。
 *          - 默认线程不安全；如需并发环境请在调用处加锁。
 */

#ifndef STACK_H
#define STACK_H

#include <stdbool.h>  /* bool   */
#include <stddef.h>   /* size_t */

#ifdef __cplusplus
extern "C" {
#endif

/** 栈元素类型（可按需修改为自定义结构体/其他标量类型） */
typedef int ElemType;

/**
 * @brief 链式栈节点
 */
typedef struct LStackNode
{
    ElemType data;             /**< 节点数据域 */
    struct LStackNode* next;   /**< 指向下一个节点（更“低”的栈元素）；栈顶节点的 next 指向次顶节点 */
} LStackNode;

/**
 * @brief 链式栈容器
 */
typedef struct LStack
{
    LStackNode* top;  /**< 栈顶指针：指向当前“最上方”的节点；空栈为 NULL */
    size_t      size; /**< 当前元素个数 */
} LStack;

/* ======================= 基础管理与状态 ======================= */

/**
 * @brief  初始化栈（置空）
 * @param  s 指向栈对象
 * @note   空栈时 top=NULL，size=0
 */
void lstack_init(LStack* s);

/**
 * @brief  销毁栈并释放所有节点
 * @param  s 指向栈对象
 * @note   逐个释放所有节点内存，结束后 top=NULL，size=0
 */
void lstack_destroy(LStack* s);

/**
 * @brief  获取当前元素个数
 * @param  s 指向栈对象（可为 NULL）
 * @return 元素个数；若 s 为 NULL 返回 0
 */
size_t lstack_size(const LStack* s);

/**
 * @brief  判断栈是否为空
 * @param  s 指向栈对象
 * @return 为空返回 true；否则返回 false
 * @warning 当前实现中若 s==NULL 将返回 false（与常见约定不同，按你现有代码语义保留）
 */
bool lstack_empty(const LStack* s);

/* ========================= 栈操作 ========================= */

/**
 * @brief  入栈：将元素压入栈顶，其实就是链表的头插法
 * @param  s     栈指针
 * @param  value 待入栈的值
 * @return 成功返回 true；分配失败或 s==NULL 返回 false
 * @complexity O(1)
 * @note   新建节点作为新的栈顶：node->next = s->top; s->top = node; size++
 */
bool lstack_push(LStack* s, ElemType value);

/**
 * @brief  出栈：弹出栈顶元素
 * @param  s         栈指针
 * @param  out_value 若非 NULL，则返回被弹出的值
 * @return 成功返回 true；空栈或 s==NULL 返回 false
 * @complexity O(1)
 * @note   弹出并释放旧栈顶节点：保存 node->data，s->top = node->next，free(node)，size--
 */
bool lstack_pop(LStack* s, ElemType* out_value);

/**
 * @brief  取栈顶元素（不弹出）
 * @param  s         栈指针（只读）
 * @param  out_value 若非 NULL，则返回栈顶值
 * @return 成功返回 true；空栈或 s==NULL 返回 false
 * @complexity O(1)
 */
bool lstack_top(const LStack* s, ElemType* out_value);

/* ========================= 调试/遍历 ========================= */

/**
 * @brief  打印栈内容（自顶向下）
 * @param  s 栈指针
 * @note   输出格式示例：顶[3, 2, 1]底 top=3 (size=3)
 */
void lstack_print(const LStack* s);

/**
 * @brief  遍历栈（自顶向下），对每个元素调用回调
 * @param  s    栈指针
 * @param  fn   回调函数：void (*)(ElemType value, void* user)
 * @param  user 透传给回调的用户参数
 * @note   回调内若修改栈需谨慎，避免破坏遍历过程
 */
void lstack_foreach(const LStack* s, void (*fn)(ElemType value, void* user), void* user);

#ifdef __cplusplus
}
#endif

#endif /* STACK_H */

linked_stack.c

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
//
// Created by keqiu on 25-10-26.
//

/**
 * @file    stack.c
 * @brief   链式栈（单链表实现）接口定义
 * @details 与 stack.h 配套的实现文件。包含初始化、销毁、入栈/出栈/取顶、
 *          判空/取大小、遍历与打印等函数的具体实现。
 */

#include "stack.h"
#include <stdlib.h>  /* malloc, free */
#include <stdio.h>   /* printf       */

/* ======================= 基础管理与状态 ======================= */

void lstack_init(LStack* s)
{
    if (s == NULL)
    {
        return;
    }

    s->top  = NULL;  /* 空栈：无节点 */
    s->size = 0;     /* 元素个数置零 */
}

void lstack_destroy(LStack* s)
{
    if (s == NULL)
    {
        return;
    }

    /* 逐个释放所有节点 */
    LStackNode* current = s->top;
    while (current != NULL)
    {
        LStackNode* next = current->next;
        free(current);
        current = next;
    }

    s->top  = NULL;
    s->size = 0;
}

size_t lstack_size(const LStack* s)
{
    if (s == NULL)
    {
        return 0;
    }

    return s->size;
}

bool lstack_empty(const LStack* s)
{
    if (s == NULL)
    {
        /* 按你现有代码：当 s==NULL 返回 false（不视为“空栈”）。
           如果你更希望 s==NULL 也判空，可改为：return true; */
        return 0;
    }

    return s->size == 0;
}

/* ========================= 栈操作 ========================= */

bool lstack_push(LStack* s, ElemType value)
{
    if (s == NULL)
    {
        return false;
    }

    /* 分配新节点并作为新的栈顶 */
    LStackNode* node = (LStackNode*)malloc(sizeof(LStackNode));
    if (node == NULL)
    {
        return false;
    }
    node->data = value;
    node->next = s->top; /* 新结点挂到当前栈顶之前 */
    s->top = node;
    s->size++;

    return true;
}

bool lstack_pop(LStack* s, ElemType* out_value)
{
    if (s == NULL || s->top == NULL)
    {
        return false;
    }

    /* 弹出并释放当前栈顶节点 */
    LStackNode* node = s->top; /* 获取目前栈顶结点 */
    if (out_value)
    {
        *out_value = node->data;  /* 返回结点数据值 */
    }
    s->top = node->next; /* 更新栈顶为下一个结点 */
    free(node);          /* 释放出栈结点内存 */
    s->size--;

    return true;
}

bool lstack_top(const LStack* s, ElemType* out_value)
{
    if (s == NULL || s->top == NULL)
    {
        return false;
    }

    if (out_value)
    {
        *out_value = s->top->data;  /* 读取栈顶结点数据值 */
    }

    return true;
}

/* ========================= 调试/遍历 ========================= */

void lstack_print(const LStack* s)
{
    if (s == NULL || s->top == NULL) {
        printf("[] top=? (size=0)\n");
        return;
    }
    /* 自顶向下打印（不进行额外内存分配），视觉上“顶”在左，“底”在右 */
    printf("顶[");
    const LStackNode* p = s->top;
    while (p != NULL)
    {
        printf("%d", p->data);
        if (p->next != NULL)
        {
            printf(", ");
        }
        p = p->next;
    }
    printf("]底 top=%d (size=%zu)\n", s->top->data, s->size);
}

void lstack_foreach(const LStack* s, void (*fn)(ElemType value, void* user), void* user)
{
    if (s == NULL || !fn) return;
    /* 自顶向下遍历；若需自底向上可先收集或使用递归（注意深度） */
    const LStackNode* p = s->top;
    while (p)
    {
        fn(p->data, user);
        p = p->next;
    }
}

测试代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
#include "stack.h"
#include <stdio.h>
#include <assert.h>

/* foreach 求和回调（自顶向下） */
static void sum_cb(int v, void* user) {
    int* acc = (int*)user;
    *acc += v;
}

int main(void) {
    LStack s;
    lstack_init(&s);

    /* 空栈状态 */
    assert(lstack_empty(&s) == true);
    assert(lstack_size(&s) == 0);
    int tmp;
    assert(lstack_pop(&s, &tmp) == false);
    assert(lstack_top(&s, &tmp) == false);

    /* 基本入栈 */
    assert(lstack_push(&s, 1) == true);
    assert(lstack_push(&s, 2) == true);
    assert(lstack_push(&s, 3) == true);
    lstack_print(&s);                        /* [1,2,3] top=3 */
    assert(lstack_size(&s) == 3);
    assert(lstack_empty(&s) == false);

    /* 取顶不弹出 */
    int topv = 0;
    assert(lstack_top(&s, &topv) == true);
    printf("top=%d\n", topv);
    assert(topv == 3);

    /* 出栈与顺序校验（LIFO） */
    int v = 0;
    assert(lstack_pop(&s, &v) == true);      /* 弹 3 */
    assert(v == 3);
    lstack_print(&s);

    assert(lstack_pop(&s, &v) == true);      /* 弹 2 */
    assert(v == 2);
    lstack_print(&s);

    assert(lstack_push(&s, 99) == true);     /* 入 99 */
    lstack_print(&s);

    /* 压入一批元素，验证增长与遍历 */
    for (int i = 0; i < 20; ++i) {
        assert(lstack_push(&s, i) == true);
    }
    lstack_print(&s);
    assert(lstack_size(&s) == 1 /* 只剩1 */ + 1 /* 99 */ + 20);

    /* foreach 求和（自顶向下） */
    int sum = 0;
    lstack_foreach(&s, sum_cb, &sum);
    printf("sum=%d\n", sum);

    /* 再弹出几个 */
    assert(lstack_pop(&s, &v) == true);
    assert(lstack_pop(&s, &v) == true);
    assert(lstack_pop(&s, &v) == true);
    lstack_print(&s);

    /* 销毁（应释放全部节点） */
    lstack_destroy(&s);
    assert(lstack_empty(&s) == true);
    assert(lstack_size(&s) == 0);
    lstack_print(&s);

    printf("All tests passed!\n");
    return 0;
}

输出结果：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
C:\Users\keqiu\myProjects\CLionProjects\C\Stack\Linked_Stack\build\Linked_Stack.exe
    
顶[3, 2, 1]底 top=3 (size=3)
top=3
顶[2, 1]底 top=2 (size=2)
顶[1]底 top=1 (size=1)
顶[99, 1]底 top=99 (size=2)
顶[19, 18, 17, 16, 15, 14, 13, 12, 11, 10, 9, 8, 7, 6, 5, 4, 3, 2, 1, 0, 99, 1]底 top=19 (size=22)
sum=290
顶[16, 15, 14, 13, 12, 11, 10, 9, 8, 7, 6, 5, 4, 3, 2, 1, 0, 99, 1]底 top=16 (size=19)
[] top=? (size=0)
All tests passed!

进程已结束，退出代码为 0

顺序栈与链式栈对比

维度 静态顺序栈（固定数组） 动态顺序栈（可扩容数组） 链式栈（单链表）
存储结构 连续内存（固定大小） 连续内存（可增长） 连续/非连续内存（结点+指针）
容量/扩展 固定上限 扩容按倍增，偶发搬移 O(n) 理论无限，受堆内存限制
push/pop O(1) 均摊 O(1)，扩容最坏 O(n) O(1)，含 malloc/free
空间开销 最小 可能有预留空闲 每元素多一个指针，含堆管理开销
是否需要手动内存分配 否（编译期/一次性固定空间） 是（malloc/realloc/free） 是（每次入/出栈涉及 malloc/free，或用内存池）
典型场景 上限已知、稳定性要求高、嵌入式 上限不明、需弹性且性能稳定 规模波动大、无需连续内存
核心优点 简单、快速、可预估 弹性好、总体性能佳 按需分配、无整体扩容
核心缺点 上限刚性、可能浪费 扩容可能致指针失效、搬移代价 碎片化、分配释放开销